이전의 글에서 신경망의 가중치는 수치 미분을 사용해서 구했습니다.
수치 미분은 단순하고 구현하기도 쉽지만 계산하는 데 시간이 오래 걸린다는 단점이 있어 이번에는 효율적으로 계산하는 방법인 '오차역전파'에 대해서 알아보겠습니다.
- 계산 그래프
- 계산 그래프는 계산 과정을 그래프로 나타낸 것으로 복수의 노드(node)와 에지(edfge)로 표현됩니다.
- 참고로 노드 사이의 직선을 에지라고 합니다.
- 계산 그래프를 사용하는 이유는 전체 그래프가 복잡하더라도 각 노드에서는 단순한 계산에 집중하여 문제를 단순화할 수 있기 때문입니다.
- 이외에도 계산 그래프를 사용하는 가장 큰 이유로는 역전파를 통해 미분을 효율적으로 계산할 수 있기 때문입니다.
- 계산 그래프 예시
- 아래의 [그림 1]에서 역전파는 오른쪽에서 왼쪽으로 '1->1.1->2.2' 순으로 미분 값을 전달합니다.
- 이 결과로부터 '사과 가격에 대한 지불 금액의 미분' 값은 2.2라고 할 수 있으며, 사과가 1원이 오르면 최종 금액은 2.2원이 오른다고 해석됩니다.
[그림 1]

- 연쇄법칙(chain rule)
- 역전파는 [그림 2]의 보라색선과 같이 국소적인 미분을 순방향과는 반대인 오른쪽에서 왼쪽으로 전달하는 것으로 전달 원리는 연쇄법칙(chain rule)에 따릅니다.
[그림 2]

- 합성 함수의 미분은 합성 함수를 구성하는 각 함수의 미분의 곱으로 나타낼 수 있으며, 이를 연쇄법칙이라고 합니다([식 1] 참고)
[식 1].

(예시)
(x+y)^2을 미분하면 2(x+y)인데 이는 연쇄법칙을 활용한 결과입니다(자세한 계산과정은 아래의 [식2] 참고).
[식 2]
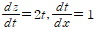

- 덧셈 노드의 역전파
- [그림 3]에서 왼쪽 그림은 순전파, 오른쪽 그림은 역전파로, 덧센 노드의 역전파는 입력 값을 그대로 흘려보낸다는 사실을 알 수 있다.
[그림 3]

- 곱셈 노드의 역전파
- 위의 그림과 동일하게 [그림 4]의 왼쪽 그림은 순전파, 오른쪽은 역전파를 나타내며, 곱셈 노드의 역전파는 상류의 값에 순전파 때의 입력 신호들을 서로 바꾼 값을 곱해서 하류로 보낸다는 사실을 알 수 있다.
[그림 4]

- 활성화 함수 - ReLU 계층
- 아래의 [식 3]의 왼쪽식은 ReLU의 수식, 오른쪽식은 왼쪽식에서 x에 대한 y의 미분 값입니다.
[식 3]

- 위의 [식 3]에서 알 수 있듯이, 순전파일 때 입력인 x가 0보다 크면 역전파는 상류의 값을 그대로 하류로 흘리며, 순전파가 0 이하이면 역전파에서는 하류로 신호를 보내지 않습니다.
- 이를 계산 그래프로 그리면 [그림 5]와 같습니다.
[그림 5]

- Softmax-with-Loss
- Softmax 계층에서는 입력 값을 정규화(출력의 합이 1이 되도록 변환)하기 때문에 출력값으로 확률을 나오도록 합니다.
- 참고로, 신경망에서 수행하는 작업은 학습과 추론이 있으며, 추론할 때는 softmax 계층을 사용하지 않습니다.
(*질문) 학습에서 softmax 계층을 사용하는 이유는?
- 소프트맥스 함수의 손실 함수로 교차 엔트로피 오차를 사용하면 역전파가 (y1-t1, y2-t2, y3-t3)로 나타나게 됨
-여기서 y는 소프트맥스의 출력, t: 정답 레이블).
(예시1)
정답 레이블: (0, 1, 0)
softmax 계층: (0.3, 0.2, 0.5)
-> softmax 계층의 역전파: (0.3, -0.8, 0.5)
(예시2)
정답 레이블: (0, 1, 0)
softmax 계층: (0.01, 0.99, 0)
-> softmax 계층의 역전파: (0.01, -0.01, 0)
- 위의 (예시1)과 (예시2)에서 알 수 있듯이, 앞 계층에서 전달된 오차가 작으면 학습하는 정도가 작아집니다.
- 오차역전파로 구한 기울기 검증하기
- 지금까지 살펴본 것처럼신경망의 가중치 및 편향을 구하는 방법은 수치 미분을 써서 구하는 방법과 오차역전파를 이용하여 계산하는 방법이 있습니다.
- 수치 미분은 느려 잘 사용되지 않지만 오차역전파의 결과와 비교하는 데 활용할 수 있습니다.
- 참고로, 수치 미분과 오차역전파의 결과 오차가 0이 되는 일은 거의 없지만 매우 작은 값이 나타나는데 이는 컴퓨터가 계산할 수 있는 수가 유한이기 떄문입니다.
출처: 사이토 고키, 「밑바닥부터 시작하는 딥러닝」, 한빛미디어(2017), p147-p187.
'딥러닝 기초' 카테고리의 다른 글
| [김기현의 딥러닝을 활용한 자연어처리] 딥러닝 환경 구축 (1) | 2023.05.11 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] 최적화 (1) | 2022.10.08 |
| [밑바닥부터 시작하는 딥러닝] 신경망에서 학습 (0) | 2022.09.18 |
| [밑바닥부터 시작하는 딥러닝] 신경망 (1) | 2022.09.04 |
| [밑바닥부터 시작하는 딥러닝] 퍼셉트론 (1) | 2022.09.03 |

