이전 글에서는 퍼셉트론에 대해서 알아보았습니다.
퍼셉트론에서는 w1, w2, b를 직접 설정해주어야 하는 번거로움이 있었는데 이번에는 데이터를 학습해 적절한 w1, w2, b의 값을 설정해주는 신경망에 대해서 알아봅시다
신경망을 이해하기 위해 활성화 함수에 대해 먼저 알아봅시다.
- 퍼셉트론 복습
- 앞의 글에서는 퍼셉트론을 [식 1]과 같이 표현하였는데 [식 2]와 같이 표현하는 것도 가능합니다.
[식 1]

[식 2]

- 활성화 함수
- 위의 [식 2]에서 h(x)를 활성화 함수(activation function)라고 하며, 입력 신호의 총합이 활성화를 일으키는지를 정하는 역할을 합니다.
- [식 2]의 활성화 함수는 [그림 1]과 같이 표현되며, '계단 함수'로 불립니다.
[그림 1] 계단 함수

- 활성화 함수로 여러가지 함수를 활용할 수 있는데 대표적으로 시그모이드 함수와 ReLU 함수가 알려져있습니다.
[그림 2] 시그모이드 함수

[그림 3] ReLU 함수

- 계단 함수와 시그모이드 함수
- 시그모이드 함수는 부드러운 곡선이며 입력에 따라 출력이 연속적으로 변화하지만 계단 함수는 0을 경계로 출력이 갑자기 바뀝니다.
- 계단 함수와 시그모이드 함수의 공통점은 둘 다 비선형 함수라는 것입니다.
- 활성화 함수의 비선형 함수
- 위에서 계단 함수와 시그모이드 함수는 모두 비선형 함수인 것이 확인되었습니다.
- 신경망에서 활성화 함수는 비선형 함수만 사용할 수 있습니다.
- 활성화 함수로 선형 함수를 활용할 경우, 신경망의 층을 깊게 하는 의미가 없어집니다.
(예시)
h(x) = cx를 활성화 함수로 사용한 3층 네트워크
이를 식으로 나타내면 y(x) = h(h(h(x))) = c*c*c*x가 되고, 이는 y(x) = ax로 표현이 가능합니다(c*c*c = a).
- 다차원 배열의 계산
[그림 4] 신경망에서 행렬 곱

X = np.array([1,2])W = np.array([[1,3,5],[2,4,6]])Y = np.dot(X,W)print(Y)[5 11 17]
> 다차원 배열의 스칼라곱을 구해주는 np.dot 함수를 사용하면 단번에 결과 Y를 계산할 수 있으며, 이는 신경망을 구현할 때 매우 중요한 역할을 합니다.
- 출력층 설계
- 신경망은 회귀와 분류 모두에 이용할 수 있으며, 일반적으로 회귀에는 항등 함수(입력 그대로를 출력)를, 분류에는 소프트맥스 함수를 사용합니다.
- 참고로, 회귀는 입력 데이터에서 연속적인 수치를 예측하는 문제이며, 분류는 데이터가 어느 클래스(class)에 속하느냐에 문제입니다.
- 소프트맥스
- 분류에서 사용하는 소프트맥스 함수의 식은 [식 3]과 같습니다.
[식 3]
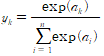
- [식 3]을 자세히 살펴보면, k번째 출력은 '모든 입력 신호의 지수 함수의 합'을 분모, 'k번째 입력 신호의 지수 함수'를 분자로 하여 계산합니다.
- 소프트맥스 함수 구현 시 주의점
- 소프트맥스 함수는 지수 함수를 사용하는데, 지수 함수는 값을 매우 크게 만듭니다.
- 예를 들어, e의 10제곱은 20,000이 넘고, e의 100제곱은 0이 40개 넘는 값이 됩니다.
- 컴퓨터는 수를 4바이트나 8바이트와 같이 크기가 유한한 데이터만 다루기 때문에 e의 1000제곱은 inf로 돌아옵니다.
- 이와 같은 문제를 해결하기 위해, 아래의 [식 4]와 같은 과정을 거칩니다.
[식 4]

> 첫 번째 변형에서 C라는 임의의 정수를 분자와 분모 양쪽에 곱했기 때문에 등호가 성립하며, 마지막 변형을 보면 소프트 맥스의 지수 함수를 계산할 때 어떤 정수를 더하거나 빼도 결과가 바뀌지 않는다는 것을 알 수 있습니다.
> 그럼 C는 어떻게 설정해야 하는지 아래의 예시를 통해 알아봅시다.
(예시)
a = np.array([1010, 1000, 990])np.exp(a) / np.sum(np.exp(a))array([nan, nan, nan]) ---> 값이 커서 계산되지 않음.
C = np.max(a)a-Carray([0, -10, -20])
np.exp(a-C) / np.sum(np.exp(a-C))
> C는 입력 신호 중 최댓값으로 설정해주면 됩니다!
- 소프트맥스 함수의 특징
- 소프트맥스 함수의 출력은 0에서 1 사이의 실수이며, 총합은 1이 됩니다.
- 위와 같은 성질로 소프트맥스 함수의 출력은 '확률'로 해석이 가능합니다.
- 예를 들어, y[0]의 확률은 0.018, y[1]의 확률은 0.245, y[2]의 확률은 0.737과 같이 해석할 수 있으며, 2반째 원소의 확률이 가장 높으니 2번째 클래스로 분류하면 됩니다.
- 여기서 주의점은 소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않아 현업에서는 지수 함수 계산에 드는 자원 낭비를 줄이기 위해 출력층의 소프트맥스 함수를 생략하기도 합니다.
- 신경망에 나오는 용어 정리
- 원-핫 인코딩(one-hot encoding): 정답을 뜻하는 원소만 1이고(hot하고), 나머지는 모두 0인 배열
(예시) 원-핫 인코딩: [0, 0, 1, 0, 0, 0, 0, 0, 0, 0] / 원-핫 인코딩X: 2
- 정규화: 데이터를 0~1과 같이 특정 범위로 변환하는 처리
- 배치(batch): 하나로 묶은 입력 데이터
> 배치 처리는 컴퓨터로 계산할 때 큰 이점을 주는데 그 이유는 컴퓨터에서는 큰 배열을 한꺼번에 계산하는 것이 분활된 작은 배열을 여러 번 계산하는 것보다 빠르기 때문입니다.
출처: 사이토 고키, 「밑바닥부터 시작하는 딥러닝」, 한빛미디어(2017), p63-p106.
'딥러닝 기초' 카테고리의 다른 글
| [김기현의 딥러닝을 활용한 자연어처리] 딥러닝 환경 구축 (1) | 2023.05.11 |
|---|---|
| [밑바닥부터 시작하는 딥러닝] 최적화 (1) | 2022.10.08 |
| [밑바닥부터 시작하는 딥러닝] 오차역전파 (0) | 2022.09.22 |
| [밑바닥부터 시작하는 딥러닝] 신경망에서 학습 (0) | 2022.09.18 |
| [밑바닥부터 시작하는 딥러닝] 퍼셉트론 (1) | 2022.09.03 |


