오늘은 심층신경망이 나오게 된 이유와 이를 행렬로 계산하는 방법에 대해서 공부하였음
대부분 이미 공부한 내용이지만 데이터가 여러 개일 때 행렬로 어떻게 계산되는지 시각적으로 볼 수 있는 기회가 되었음
7-1. 퍼셉트론
1. 퍼셉트론
- 퍼셉트론은 프랑크 로젠블라트가 1957년에 제안한 초기 형태의 인공신경망으로 다수의 입력으로부터 하나의 결과를 내보내는 알고리즘
- 각 입력값이 가중치와 곱해져서 인공 뉴런에 보내지고, 각 입력값과 그에 해당되는 가중치의 곱의 전체 합이 임계치를 넘으면 종착지에 있는 인공 뉴런은 출력 신호로서 1을 출력, 그렇지 않을 경우에는 0을 출력

- 이때 뉴런에서 출력값을 변경시키는 함수를 활성화함수라고 함
- 퍼셉트론의 활성화함수는 계단 함수이지만 시그모이드 함수로 변경하면 로지스틱 회귀와 동일
2. 단층 퍼셉트론
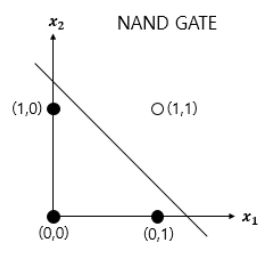
- 단층 퍼셉트론을 이용하면 AND, NAND, OR 게이트는 구현이 가능하지만 XOR게이트는 구현 불가
- AND 게이트는 입력값이 모두 1인 경우에만 출력값이 1이 나오는 구조
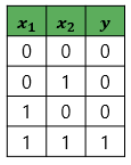

- NAND 게이트는 두 개의 입력값이 1인 경우에만 0이 나오는 구조

- OR 게이트는 두 개의 입력값이 모두 0인 경우에만 출력값이 0인 구조


- XOR 게이트는 입력값 두 개가 서로 다른 값을 갖고 있을 때만 출력값이 1이 되고, 입력값 두 개가 서로 같은 값을 가지면 출력값이 0이 되는 구조

3. 다층 퍼셉트론
- 다층 퍼셉트론은 단층 퍼셉트론에 은닉층을 추가한 형태이며, XOR 문제를 해결
- 이와 같이 은닉층이 2개 이상인 신경망을 심층 신경망(Deep Neural Network, DNN)이라고 함
- 학습을 시키는 인공 신경망이 심층 신경망일 경우에 딥러닝이라고 함

7-2. 인공 신경망
1. 피드 포워드 신경망(Feed-Forward Neural Network, FFNN)
- 다층 퍼셉트론과 같이 오직 입력층에서 출력층 방향으로 연산이 전개되는 신경망을 피드 포워드 신경망이라고 함

- RNN은 은닉층의 출력값을 출력층으로도 값을 보내지만, 동시에 은닉층의 출력값이 다시 은닉층의 입력으로 사용

2. 전결합층(Fully-connected layer)
- 어떤 층의 모든 뉴런이 이전 층의 모든 뉴런과 연결돼 있는 층을 전결합층 또는 완전연결층이라고 함
- 다층 퍼셉트론의 모든 은닉층과 출력층은 전결합층이며, 동일한 의미로 밀집층이라고 부르기도 함
3. 활성화 함수
- 활성화 함수는 선형 함수가 아닌 비선형 함수(선형 함수로 은닉층을 여러번 추가하면 1회 추가한 것과 차이가 없음)
예) 활성화 함수 f(x) = 2x라고 하면, 은닉층을 여러 번 추가하면 f(x) = 2*2*2*x -> f(x) = 8x로 가능
- 활성화 함수의 예시는 [딥러닝 파이토치 교과서] 활성화함수와 손실 함수 (tistory.com) 참고
7-3. 행렬곱으로 이해하는 신경망
1. 순전파(Foward Propagation)
- 입력값은 입력층, 은닉층을 지나면서 각 층에서의 가중치와 함께 연산되며 출력층으로 향하고, 출력층에서 모든 연산을 마친 예측값이 나옴
- 이와 같이 입력층에서 출력층 방향으로 예측값의 연산이 진행되는 과정을 순전파라고 함
2. 행렬곱으로 순전파 이해
- 입력의 차원이 3, 출력의 차원이 2인 인공 신경망은 아래와 같음(1개의 데이터)



3. 행렬곱으로 병렬 연산 이해
- 인공 신경망을 행렬곱으로 구현할 떄의 흥미로운 점은 행력곱을 사용하면 병렬 연산도 가능
- 아래의 그림은 입력의 차원이 3, 출력의 차원이 2인 인공신경망 (4개의 데이터)
- 여기서 주의할 점은 인공 신경망은 4개의 샘플을 동시에 처리하고 있지만, 여기서 학습가능한 매개변수의 수는 여전히 8개라는 점(이렇게 인공 신경망이 다수의 샘플을 동시에 처리하는 것을 '배치 연산'이라고 함)

4. 행렬곱으로 다층 퍼셉트론의 순전파 이해


출처: 유원준/안상준, 딥러닝을 이용한 자연어 처리 입문-1권, p240-p284.
'자연어 처리' 카테고리의 다른 글
| [딥러닝을 이용한 자연어 처리 입문] 센텐스버트 (0) | 2023.05.29 |
|---|---|
| [웹 크롤링] selenium을 이용한 웹크롤링 (0) | 2023.05.29 |
| [딥러닝을 이용한 자연어 처리 입문] 소프트맥스 회귀 (0) | 2023.04.16 |
| [딥러닝을 이용한 자연어 처리 입문] 벡터와 행렬 연산 (0) | 2023.04.16 |
| [딥러닝을 이용한 자연어 처리 입문] 선형 회귀와 로지스틱 회귀 (0) | 2023.04.16 |


